SOBRE CÁLCULO DE INTERÉS EN LOS PRÉSTAMOS DE CUOTA CONSTANTE COMPRENSIVA DE CAPITAL E INTERESES

ANTONIO YAGO ORTEGA, NOTARIO DE MURCIA

 

 

Estas notas están basadas en el análisis de un caso práctico real.

Las cifras que se manejan son reales, extraídas de ese caso, pero sus resultados -habida cuenta de la uniformidad de las minutas o modelos de prestamos personales e hipotecarios– son extrapolables a varias entidades financieras españolas que siguen ese modelo, aunque no a todas.

 

I.- La practica objeto del presente análisis consiste en que en la misma escritura de préstamo hipotecario se insertan dos formulas matemáticas que resultan incongruentes, a saber, una formula matemática que denominaremos a) que sirve para calcular el importe de la cuota mixta comprensiva de capital e interés y otra formula que denominaremos b) que sirve para efectuar la liquidación de intereses exclusivamente.

La formula (a) para calcular el importe de la cuota constante en el caso que sirve de base a estas notas se trascribe de los libros de matemática financiera en la escritura así:

 

 

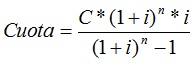
         Donde C es el capital pendiente de amortizar o devolver, i es el tipo de interés nominal expresado en tanto por uno y n es el número de liquidaciones que faltan hasta el vencimiento final de la operación

 

La formula (b) para el cálculo de intereses (operación que evidentemente ya está implícita en la formula anterior, aunque de forma distinta, como veremos, de ahí la oscuridad e incongruencia que denunciamos) en el mismo caso practico y, por cierto, en el párrafo siguiente, se recoge diciendo que los intereses se devengaran por días y su liquidación se producirá con la misma periodicidad (en el caso, mensualmente) mediante la aplicación de la siguiente formula (b):

 

 

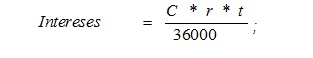
Donde C es el Principal pendiente del préstamo (lógicamente al principio de mes), R = Tipo de interés anual nominal (en tanto por ciento), T = Número de días del mes natural de que se trate, aclarando adicionalmente la escritura que el computo será el ordinario anual de 365 días y en los años bisiestos de 366.

 

II.- En el caso base del presente análisis, al tiempo del otorgamiento de la escritura de novación de préstamo hipotecario o para ser más preciso en el instante siguiente al otorgamiento de la misma las características del préstamo eran las siguientes:

 

         – Capital pendiente de amortizar: 673.070’30€.

         – Tipo de interés fijo: 3{81190e917790475744d1d81edcc4d7d0110a571f4848b7a9ee305cbac1831039} nominal anual.

         – Plazo: 234 meses.

 

         Las cuotas eran mensuales fijas comprensivas de capital e interés.

 

         La aplicación de la formula (a) al préstamo de las características expresadas nos lleva a una cuota mixta mensual de 3.802’77€ y a un cuadro que también llamaremos (A) del que insertamos a continuación las cifras de las primeras doce cuotas:

 

CUADRO A

Fecha	Cuota total	intereses	Capital
10/03/2017	3.802,77 €	1.682,68 €	2.120,09 €
10/04/2017	3.802,77 €	1.677,38 €	2.125,39 €
10/05/2017	3.802,77 €	1.672,06 €	2.130,70 €
10/06/2017	3.802,77 €	1.666,74 €	2.136,03 €
10/07/2017	3.802,77 €	1.661,40 €	2.141,37 €
10/08/2017	3.802,77 €	1.656,04 €	2.146,72 €
10/09/2017	3.802,77 €	1.650,67 €	2.152,09 €
10/10/2017	3.802,77 €	1.645,29 €	2.157,47 €
10/11/2017	3.802,77 €	1.639,90 €	2.162,87 €
10/12/2017	3.802,77 €	1.634,49 €	2.168,27 €
10/01/2018	3.802,77 €	1.629,07 €	2.173,69 €
10/02/2018	3.802,77 €	1.623,64 €	2.179,13 €

 

         La entidad financiera acreedora emite un cuadro de amortización que llamamos (B) en el que la cuota mixta constante o fija es de 3.817’17€ cuyas doce primeras cuotas transcribimos a continuación porque también son suficientes para evidenciar las consecuencias de este distinto modo de calcular:

 

CUADRO B

Fecha	Cuota total	intereses	Capital
10/03/2017	3.817,17 €	1.570,50 €	2.246,67 €
10/04/2017	3.817,17 €	1.732,96 €	2.084,21 €
10/05/2017	3.817,17 €	1.671,85 €	2.145,32 €
10/06/2017	3.817,17 €	1.722,03 €	2.095,14 €
10/07/2017	3.817,17 €	1.661,25 €	2.155,92 €
10/08/2017	3.817,17 €	1.711,05 €	2.106,12 €
10/09/2017	3.817,17 €	1.705,61 €	2.111,56 €
10/10/2017	3.817,17 €	1.645,31 €	2.171,86 €
10/11/2017	3.817,17 €	1.694,55 €	2.122,62 €
10/12/2017	3.817,17 €	1.634,58 €	2.182,59 €
10/01/2018	3.817,17 €	1.683,42 €	2.133,75 €
10/02/2018	3.817,17 €	1.677,91 €	2.136,26 €

 

         La primera de las cuotas transcritas es ligeramente anómala porque su duración fue inferior a un mes (en la novación se cambió el día de vencimiento mensual) y por tanto se liquidaron intereses por menos tiempo y cantidad aplicándose el resto de la cuota que sí es igual a todas las demás a amortizar capital. Nótese que este honrado modo de proceder debería haber producido una insignificante disminución del importe de las cuotas mixtas respecto de las que resultan de la formula (a) del cuadro (A), lo que refuerza las conclusiones de este trabajo.

 

III.- Comparando y examinando los transcritos cuadros (A) y (B) observamos:

         1º) La cuota fija del cuadro (A) es de un importe inferior a la del cuadro (B) que aplica y entrega la entidad financiera en la cifra de 14’40€, lo que multiplicado por las 234 cuotas de duración del préstamo da la cifra de 3.369’60€, que la entidad financiera cobra de más respecto de lo que cobraría con la aplicación lisa y llana de la formula (A) que genera sin duda el cuadro (A) de amortización.

         2º) La formula (a) y el cuadro (A) aplican lisa y llanamente a la amortización el interés mensual anual pactado del 3{81190e917790475744d1d81edcc4d7d0110a571f4848b7a9ee305cbac1831039}. – En su consecuencia dividen ese interés en 12 partes iguales y consideran iguales los 12 meses del año. Como consecuencia de todo ello el componente de interés va descendiendo paulatinamente, pero sin excepción ninguna, en las sucesivas cuotas de amortización aumentando del mismo modo y en igual medida del componente de capital de las cuotas.  

         Por el contrario, en el cuadro (B) se observa que en ciertos meses el componente de intereses sube respecto del de los meses anteriores, a pesar de que el capital pendiente es inferior. – Por ejemplo, la cuota de 10-VIII-2017 en este cuadro (B) tiene un componente de intereses de 1.711’05€ superior claramente a la de la anterior cuota de 10-VII-2017 cuyo componente de intereses es de 1661’25€ (49’80 € menos).

         3º) El cuadro (B) es perfectamente coherente con la formula (b), pero no con la formula (a), consistiendo sustantivamente esa incoherencia con la formula (a) en la diferencia del importe de las cuotas que hemos expresado en el párrafo 1º) anterior.

         La coherencia del cuadro (B) con la formula (b) explica no solo los ocasionales aumentos del componente de interés en cuotas posteriores que ya hemos apuntado, sino sobre todo el aumento de intereses que devengan ya que al considerar el año de 360 días cada año no se cobra exactamente el 3{81190e917790475744d1d81edcc4d7d0110a571f4848b7a9ee305cbac1831039}, sino el 3{81190e917790475744d1d81edcc4d7d0110a571f4848b7a9ee305cbac1831039} más los intereses de 5 días, o de 6 si el año es bisiesto. Esos intereses de más que se cobran con la formula (b), el cuadro (B), suman en su caso como hemos dicho, 3.369’60€ en el conjunto de la vida del préstamo.

 

IV.- Lo dicho hasta aquí nos lleva a la pregunta crucial de este trabajo: ¿cómo llega la entidad financiera a obtener el importe de la cuota fija que le permite elaborar y aplicar un cuadro (B) rigurosamente coherente con la formula (b) que junto con la formula (a) aparece inserta en la minuta de sus préstamos?

         Según nuestros conocimientos de matemáticas financieras, que se limitan al bachillerato de ciencias de la época 1957-1964, no hay más formula para averiguar la cuota fija constante del llamado sistema francés que la formula (a) y esa en el caso de que hablamos nos lleva sin duda a una cuota mensual de 3.802’77€ y a un cuadro que es el (A).

         La respuesta está en que se utiliza esa formula (a), pero se le introduce un tipo de interés que no es el 3{81190e917790475744d1d81edcc4d7d0110a571f4848b7a9ee305cbac1831039} nominal anual pactado expresamente, sino el resultado de multiplicar el interés pactado (único que debe aplicarse) por la fracción:

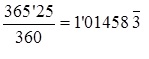
         Si la formula (a) se le introduce como tipo de interés el 3’04374 (que es el resultado de multiplicar 3 por 1’01458) la cuota fija resultante es la que aparece en el cuadro (B) de amortización, que facilita y usa la cantidad financiera del caso, es decir, 3.817’17€.

         Esa operación, a nuestro juicio indebida, se pretende justificar con la adecuación a la formula (b) de calculo de intereses que se basa en una ficción (año de 360 días) que carece de explicación hoy con los medios de calculo electrónicos que están al alcance de todos.

 

V.- Conclusiones practicas para Notarios y Registradores.

         1º) En las escrituras y pólizas de prestamos que siguen el modelo del caso base del presente trabajo, la entidad que redacta ese modelo introduce dos formulas que son incompatibles entre si y que conducen a resultados distintos.

         Para resolver esa antinomia en beneficio propio, desde luego la entidad financiera introduce en la formula (a) como hemos visto un tipo de interés superior al pactado y con eso obtiene una cuota que le permite elaborar y aplicar un cuadro de amortización (B) que resiste perfectamente todas las comprobaciones que se le quieran hacer aplicando la formula (b) a todas y cada una de las cuotas que lo integran.

         Como la formula (a) es muy compleja para hacerla “manualmente” los prestatarios de nivel matemático normal se limitan como máximo a introducir las variables en alguna de las versiones que circulan en Internet de la formula (a) y comprueban que aunque la cuota que les sale a ellos es inferior a la de la entidad financiera, es solo ligeramente inferior y entonces a lo sumo, y teniendo en cuenta que la formula (b) es asequible a todo el mundo para su aplicación “manual” comprueban que todas las cuotas que revisan del cuadro (B) se ajustan y soportan perfectamente la aplicación de la formula (b), con lo cual se conforman y piensan que esa pequeña diferencia tal como suelen decir en las entidades financieras “es cosa de los ordenadores”. Con los ordenadores actuales estas “cosas” no son de ellos, si no de quienes los programan o los utilizan y les introducen los datos. Quizás los ordenadores del futuro hagan estas “cosas” ellos solitos.

         Este proceder matemático para el cálculo de los intereses de los préstamos es engañoso, porque oculta al prestatario el tipo de interés que se introduce en la formula (a) para averiguar la cuota, es de notable sutileza, ya que la pequeña alteración del tipo de interés se hace al aplicar la formula (a) de considerable complejidad, ofreciendo al prestatario un cuadro de amortización (B) que resiste perfectamente todas las aplicaciones que se le quieren hacer con la sencilla formula (b). Como, por otra parte, las diferencias no son groseras, pueden permanecer ocultas al prestatario durante muchos años, en cuanto se haya acostumbrado a pagar la cuota averiguada por la entidad financiera.

         Esa incongruencia o ambigüedad de las formulas y ese poco claro proceso matemático debe ser objeto como mínimo de advertencia por el Notario y en su caso, de calificación por el Registrador. Esto significa que en cada Notaria y en cada Registro de la Propiedad debe haber una conexión o un medio informático con la formula correcta del calculo de las cuotas debidamente contrastada aplicándolo a cada caso para comprobar la exactitud o inexactitud de la cuota mixta que facilita la entidad financiera. En esta página de “notariosyregistradores” existe un enlace al programa informático facilitado por el Banco de España donde fácilmente se puede comprobar y verificar todo lo expuesto anteriormente.

Los prestatarios medios no detectan esa ambigüedad y por tanto están firmando un préstamo sin conocer completamente las características del mismo y sus consecuencias por eso debe el Notario servidor de la verdad y de la calidad de los consentimientos darle la información que le oculta la entidad financiera y en el caso de los prestamos hipotecarios entendemos que el Registrador cuando la cuota de amortización no sea la que corresponde a las variables del préstamo aplicando la formula correcta (salvo variaciones verdaderamente insignificantes) debe hacer lo mismo que hace cuando en una división de finca la suma de la superficie de las resultantes no coincide con la superficie de la matriz.

         En este asunto ocurre exactamente al revés que en el de las cláusulas suelo donde es evidente que la inmensa mayoría, por no decir la totalidad de los prestatarios firmaron perfectamente conscientes del significado y alcance de esas cláusulas. 

 

 ENLACES:

SIMULADORES CÁLCULO CUOTA HIPOTECA

FICHA CLÁUSULA 360 DÍAS

SECCIÓN CONSUMO Y DERECHO

Beneficio de exoneración del pasivo insatisfecho y acuerdo extrajudicial de pagos.

NORMAS:   Cuadro general.     Por meses.     + Destacadas

NORMAS:   Resúmenes 2002 – 2017.   Futuras.   Consumo

NORMAS:   Tratados internacionales,  Derecho Foral,  Unión Europea

RESOLUCIONES:    Por meses.   Por titulares.  Índice Juan Carlos Casas

WEB:   Qué ofrecemos  NyR, página de inicio   Ideario

CASOS PRÁCTICOS:   Madrid y Bilbao.    Internacional.

IR ARRIBA